what is standard deviation in relation to mean
Standard Deviation | A Step by Step Guide with Formulas
The standard deviation is the average corporeality of variability in your dataset. It tells you, on average, how far each value lies from the mean.
A loftier standard difference means that values are by and large far from the mean, while a low standard departure indicates that values are clustered shut to the mean.
What does standard deviation tell y'all?
Standard difference is a useful mensurate of spread for normal distributions.
In normal distributions, data is symmetrically distributed with no skew. Most values cluster around a cardinal region, with values tapering off as they go further away from the center. The standard divergence tells you lot how spread out from the center of the distribution your data is on boilerplate.
Many scientific variables follow normal distributions, including height, standardized test scores, or job satisfaction ratings. When you lot accept the standard deviations of dissimilar samples, you tin compare their distributions using statistical tests to make inferences near the larger populations they came from.
The mean (G) ratings are the same for each group – it's the value on the x-axis when the curve is at its height. However, their standard deviations (SD) differ from each other.
The standard deviation reflects the dispersion of the distribution. The curve with the lowest standard divergence has a high peak and a pocket-sized spread, while the bend with the highest standard deviation is more flat and widespread.

The empirical rule
The standard deviation and the mean together can tell you where most of the values in your distribution lie if they follow a normal distribution.
The empirical rule, or the 68-95-99.7 rule, tells y'all where your values lie:
- Around 68% of scores are within 1 standard deviation of the mean,
- Around 95% of scores are inside 2 standard deviations of the mean,
- Around 99.7% of scores are within 3 standard deviations of the mean.
Following the empirical dominion:
- Around 68% of scores are between twoscore and threescore.
- Around 95% of scores are between 30 and lxx.
- Effectually 99.7% of scores are between 20 and 80.
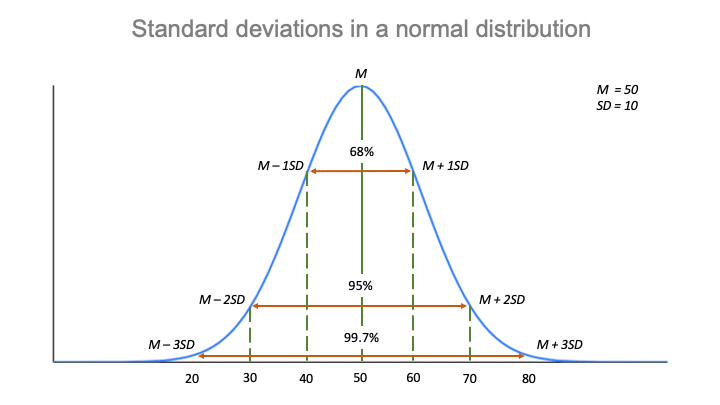
The empirical rule is a quick manner to get an overview of your information and check for whatever outliers or extreme values that don't follow this pattern.
For not-normal distributions, the standard deviation is a less reliable measure of variability and should be used in combination with other measures similar the range or interquartile range.
Standard deviation formulas for populations and samples
Unlike formulas are used for calculating standard deviations depending on whether you take data from a whole population or a sample.
Population standard deviation
When you accept nerveless data from every member of the population that you're interested in, yous can get an exact value for population standard deviation.
The population standard deviation formula looks like this:
| Formula | Caption |
|---|---|
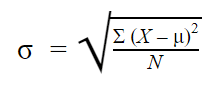 |
|
Sample standard difference
When you collect data from a sample, the sample standard departure is used to make estimates or inferences nigh the population standard departure.
The sample standard deviation formula looks like this:
| Formula | Explanation |
|---|---|
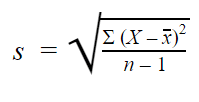 |
|
With samples, we use n – one in the formula because using n would give u.s.a. a biased judge that consistently underestimates variability. The sample standard difference would tend to be lower than the real standard deviation of the population.
Reducing the sample due north to northward – ane makes the standard difference artificially large, giving you lot a conservative estimate of variability.
While this is not an unbiased estimate, information technology is a less biased approximate of standard divergence: it is ameliorate to overestimate rather than underestimate variability in samples.
Steps for calculating the standard deviation
The standard deviation is commonly calculated automatically by whichever software you utilise for your statistical analysis. But yous tin also summate it by hand to ameliorate empathise how the formula works.
There are 6 chief steps for finding the standard divergence past hand. Nosotros'll use a pocket-size data set of 6 scores to walk through the steps.
| Data set | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | sixty | 52 | 41 |
Step one: Notice the hateful
To find the mean, add together upward all the scores, then divide them past the number of scores.
| Mean (x̅) |
|---|
| x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50 |
Step 2: Find each score'south deviation from the mean
Decrease the mean from each score to get the deviations from the mean.
Since x̅ = 50, here we have abroad 50 from each score.
| Score | Deviation from the mean |
|---|---|
| 46 | 46 – fifty = -4 |
| 69 | 69 – fifty = 19 |
| 32 | 32 – l = -18 |
| threescore | lx – 50 = 10 |
| 52 | 52 – fifty = 2 |
| 41 | 41 – 50 = -ix |
Step iii: Square each deviation from the mean
Multiply each deviation from the mean past itself. This volition issue in positive numbers.
| Squared deviations from the hateful |
|---|
| (-4)2 = 4 × iv = sixteen |
| xix2 = xix × 19 = 361 |
| (-18)ii = -18 × -18 = 324 |
| 102 = ten × x = 100 |
| ii2 = 2 × ii = 4 |
| (-ix)two = -9 × -9 = 81 |
Pace four: Find the sum of squares
Add upwardly all of the squared deviations. This is chosen the sum of squares.
| Sum of squares |
|---|
| 16 + 361 + 324 + 100 + 4 + 81 = 886 |
Step 5: Find the variance
Divide the sum of the squares past n – 1 (for a sample) or N (for a population) – this is the variance.
Since we're working with a sample size of 6, we volition use n – 1, where northward = vi.
| Variance |
|---|
| 886 ÷ (6 – ane) = 886 ÷ 5 = 177.2 |
Stride half dozen: Find the foursquare root of the variance
To observe the standard divergence, we take the foursquare root of the variance.
| Standard deviation |
|---|
| √177.two = thirteen.31 |
From learning that SD = 13.31, we can say that each score deviates from the mean by xiii.31 points on average.
Why is standard difference a useful measure of variability?
Although in that location are simpler ways to calculate variability, the standard divergence formula weighs unevenly spread out samples more than evenly spread samples. A higher standard divergence tells y'all that the distribution is not only more spread out, but also more unevenly spread out.
This means it gives you a meliorate idea of your information'southward variability than simpler measures, such every bit the mean absolute deviation (MAD).
The MAD is similar to standard departure only easier to summate. First, you lot limited each divergence from the mean in absolute values by converting them into positive numbers (for instance, -3 becomes three). Then, you calculate the hateful of these absolute deviations.
Unlike the standard divergence, you don't take to calculate squares or foursquare roots of numbers for the MAD. However, for that reason, information technology gives you a less precise mensurate of variability.
Allow'south take two samples with the same primal tendency but dissimilar amounts of variability. Sample B is more variable than Sample A.
| Values | Mean | Mean absolute deviation | Standard departure | |
|---|---|---|---|---|
| Sample A | 66, 30, 40, 64 | 50 | xv | 17.eight |
| Sample B | 51, 21, 79, 49 | 50 | 15 | 23.7 |
For samples with equal average deviations from the mean, the MAD can't differentiate levels of spread. The standard departure is more precise: it is college for the sample with more variability in deviations from the mean.
By squaring the differences from the hateful, standard deviation reflects uneven dispersion more accurately. This step weighs extreme deviations more heavily than modest deviations.
Nonetheless, this also makes the standard deviation sensitive to outliers.
Ofttimes asked questions about standard divergence
- What does standard deviation tell you?
-
The standard divergence is the boilerplate corporeality of variability in your data set. It tells yous, on average, how far each score lies from the hateful.
In normal distributions, a loftier standard difference means that values are more often than not far from the mean, while a low standard divergence indicates that values are amassed close to the hateful.
- What is the empirical rule?
-
The empirical rule, or the 68-95-99.vii rule, tells you where near of the values prevarication in a normal distribution:
- Around 68% of values are within i standard departure of the mean.
- Around 95% of values are inside 2 standard deviations of the mean.
- Around 99.7% of values are within 3 standard deviations of the mean.
The empirical rule is a quick way to get an overview of your data and check for whatsoever outliers or extreme values that don't follow this pattern.
Is this commodity helpful?
Yous have already voted. Thanks :-) Your vote is saved :-) Processing your vote...
Source: https://www.scribbr.com/statistics/standard-deviation/
Post a Comment for "what is standard deviation in relation to mean"